DeepMedic - multi-sacle 3D CNN with CRF for brain lesion segmentation

DeepMedic - multi-sacle 3D CNN with CRF for brain lesion segmentation

   Zhanhang (Matthew) ZENG 16 minutes read (About 2365 words)  0 visits
 Computer Vision / Networks Architecture 

论文阅读笔记，如果我有什么理解错误的地方，欢迎大家指正。
论文：Efficient multi-scale 3D CNN with fully connected CRF for accurate brain lesion segmentation

摘要：作者提出一种双路径，11层深的3D卷积神经网络用于brain lesion segmentation任务，主要解决了医学图像处理上的三个方面的问题。一是作者设计了一种dense training scheme的方案，采用全卷积神经网络，一次把相邻像素的image segments传入网络输出dense prediction (dense-inference)，从而节省了计算代价。作者使用更深的网络使模型判别能力更强。作者使用一种dual pathway architecture，即同时训练两个网络，使模型同时对高/低分辨率图像进行处理。最后作者采用全连接条件随机场(Fully connected Conditional Random Field)对网络output进行后处理(post-processing)改善图像类之间的边缘信息。

1. Dense Training

在传统patch-wise的分类中，输入patch的尺寸和cnn最后一层神经元的感受野大小相同，这样网络得到一个single prediction对应输入patch的中心像素的值。而用全卷积实现的神经网络，因为其输入的patch的尺寸可以大于最后一层神经元的感受野，因此模型可以同时输出多个prediction，即dense-inference，而每一个prediction对应cnn’s receptive field的在输入patch上的每一步stride。


Fig.2. Our baseline CNN consists of four layers with $5^3$ kernels for feature extraction, leading to a receptive field of size $17^3$. The classification layer is implemented as convolutional with $1^3$ kernels, which enables efficient dense-inference. When the network segments an input it predicts multiple voxels simultaneously, one for each shift of its receptive field over the input. Number of FMs and their size depicted as (Number × Size).

同时作者认为，这样dense-inference得到的每一个prediction都是可信的，只要感受野是完全在input patch上扫过，并且只捕捉到原始信息，因此没有使用padding。

Dense Training Scheme 的优点

  • 节省计算代价和内存消耗
  • 灵活：作者提到最佳的性能为将整个图像送入网络，但是这个做法不现实。如果GPU内存限制不允许，例如在需要缓存大量FM的大型3D网络的情况下，则将图像分成多个image-segments，这样会比单个segment大，但是可以去fit内存。（原文：If GPU memory constraints do not allow it, such as in the case of large 3D networks where a large number of FMs need to be cached, the volume is tiled in multiple image-segments, which are larger than individual patches, but small enough to fit into memory.）

CNNs are trained patch-by-patch: 个人认为论文中提到的这个操作是在图像上randomly crop出一个individual patch作为网络的输入来训练网络，以此计算loss和进行gradient descent。

2. Class Balance

(这里不太确定自己理解对不对)

在原文的Section 2.2中作者提到，这种dense training scheme的方案中的sampling input segments (即上面提到的randomly crop individual patches) 提供了一种灵活的方式去平衡training samples中的segmentation classes（正负类）的分布，而不同的分布对模型的性能有很大的影响。

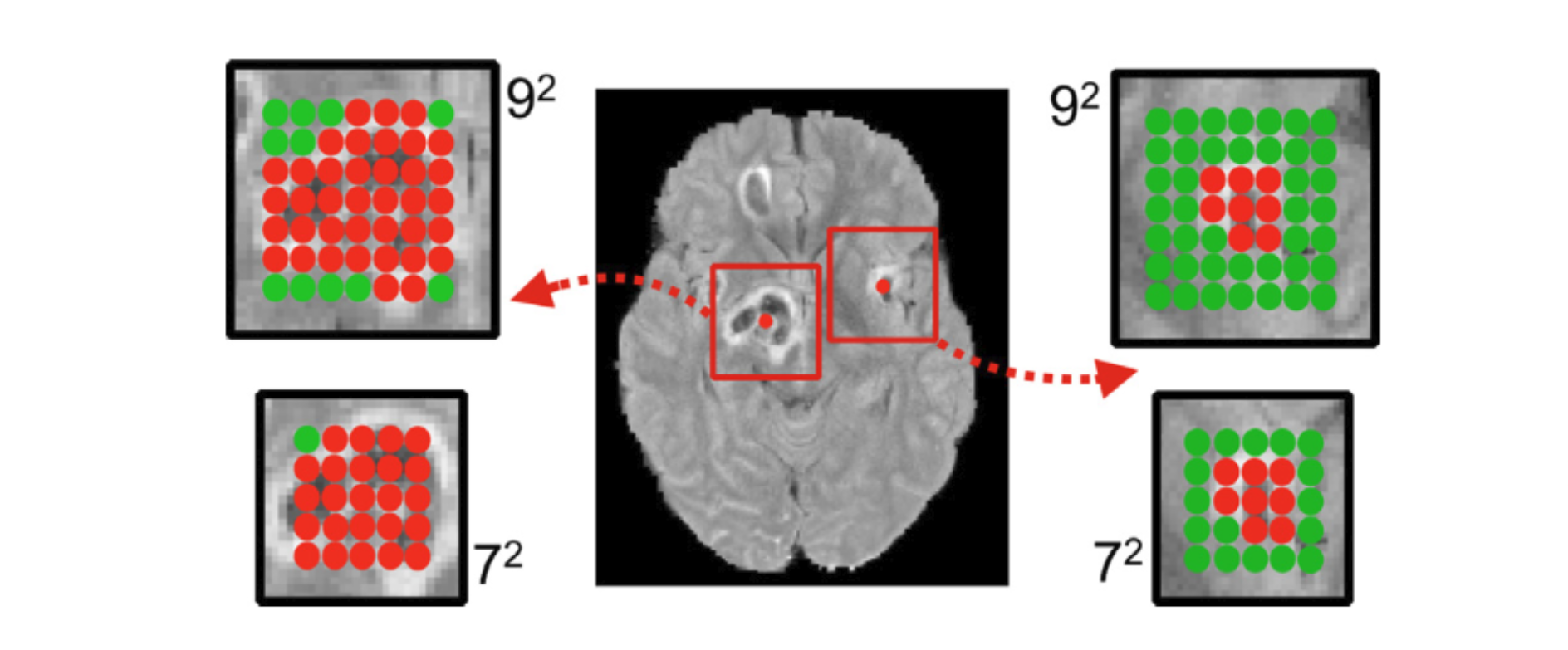
Fig.3. Consider a network with a 2D receptive field of $3^2$ (for illustration) densely-applied on the depicted lesion-centred image segments of size $7^2$ or $9^2$. Relatively more background (green) is captured by larger segments and around smaller lesions. (For interpretation of the references to colour, the reader is referred to the web version of this article.)

从上图和原文Section 3.2的实验结果来看，感觉有点类似过采样的意思。上图说明，如果是crop一个以病变为中心 (lesion-centered) 的image segments，分别用 $7 \times 7$ 和 $9 \times 9$ 的框去crop下来，可以看到用 $9 \times 9$ 的框去crop出这个image segment的话，绿色的内容会相对更多一点。

作者在Section 3.2的最后一段也提到，这个segments size在模型中是一个超参数，提到segment size会提升模型的性能，但是很快这种性能的提升久会达到平稳(level off)，并且在一系列的segment size中都会得到相似的性能。

3. 构建更深的网络

该部分总结：Deeper Networks + Smaller Kernel + Batch Norm + (p)ReLU + $ \mathcal{N}\left(0,\ \sqrt{2/n^{in}_{l}} \right)$

更深的网络有更好的判别能力，但是更深的网络同时意味着更高的计算代价和更吃内存。所以在这里作者采用的策略是层数增加，但是把kernel size从 $5^3$ 缩小到 $3^3$ 从而减少计算代价和节省内存。作者认为这里kernel size减小说明需要训练的parameters的数量减少，一定程度上有正则的效果。（但是原文好像只是给了个简单的 $\frac{5^3}{3^3} \approx 4.6$，但是层数的增加会增加参数的数量，不知道作者有没有算对，我也没去算它….）

因为更深的网络变得容易train不下去，所以作者采用了 ReLU-based 的网络 (在github文件看，DeepMedic的网络好像采用的是pReLU)。同时，作者不采用标准正态分布去初始化kernel weights，才是采用了 $ \mathcal{N}\left(0,\ \sqrt{2/n^{in}_{l}} \right)$ 。

Batch Normalisation

4. Dual Pathways Networks



Fig.5. Multi-scale 3D CNN with two convolutional pathways. The kernels of the two pathways are here of size $5^3$ (for illustration only to reduce the number of layers in the figure). The neurons of the last layers of the two pathways thus have receptive fields of size $17^3$ voxels. The inputs of the two pathways are centred at the same image location, but the second segment is extracted from a down-sampled version of the image by a factor of 3. The second pathway processes context in an actual area of size $51^3$ voxels. DeepMedic, our proposed 11-layers architecture, results by replacing each layer of the depicted pathways with two that use $3^3$ kernels (see Section 2.3). Number of FMs and their size depicted as (Number × Size).

作者为上述deeper networks增加了第二个pathway networks，对down-sampling的图像进行操作。这种dual pathways 3D CNN 同时对高/低分辨率图像进行训练，文中提到第二个网络(低分辨率)用于捕捉一些high level的信息，例如 location。而第一个网络（高分辨率）用于捕捉一些细节信息。为了使得最后输出的feature maps尺寸一致，要对第二个网络的输出进行上采样以匹配第一个网络输出的feature maps的尺寸。

5. 3D fully connected CRF

作者认为CNN网络输出的结果偏向与smooth（如何smooth可以见下图），因此对DeepMedic网络（11层，dual pathways）网络的输出认为是soft segmentation。最后作者用CRF对soft segmentations 进行后处理（post-processing）改善其边缘信息。


5.1 为什么CRF可以用于处理图像任务？

首先对于图像任务，我们可以把每个像素认为是一个单独的节点（node），像素与像素之间就构成了边（edge），同时，相邻像素之间相互影响，而这种影响是对称的，相当于edge，因此构成了一个概率无向图。

5.2 全连接条件随机场

对于每个像素 $i$ 具有类别标签 $x_i$ 还有对应的观测值 $y_i$，这样每个像素点作为节点，像素与像素间的关系作为边，即构成了一个条件随机场。而且我们通过观测变量 $y_i$ 来推测像素 $i$ 对应的类别标签 $x_i$。条件随机场如下：

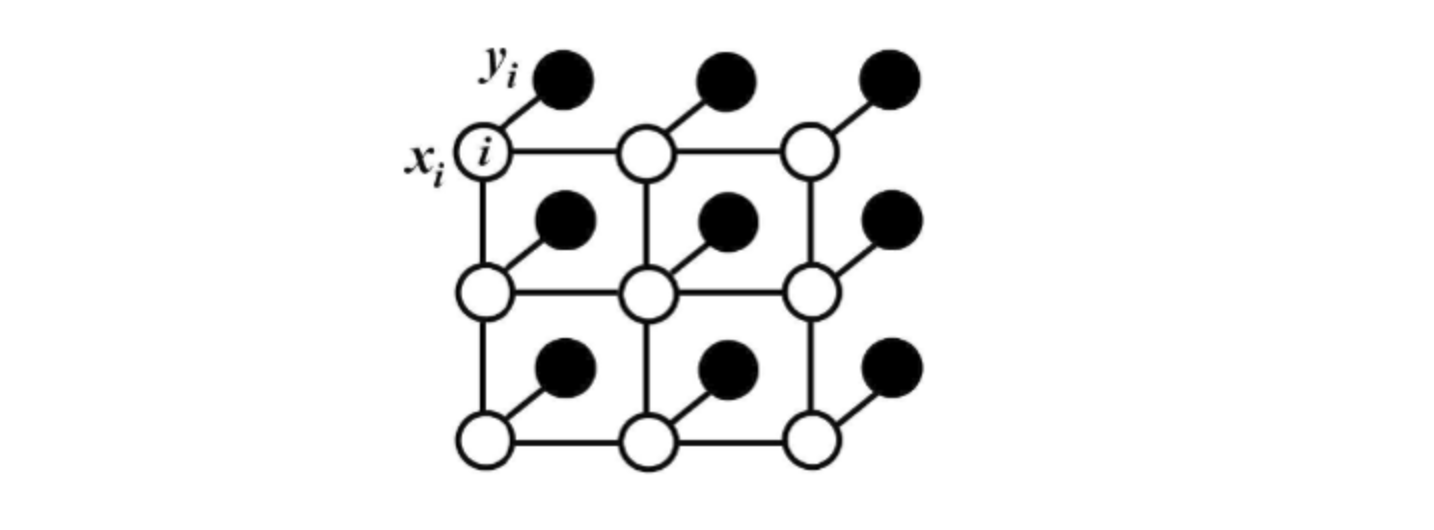
条件随机场符合吉布斯分布：(此处的 $x$ 即上面说的观测值)
$$P(\boldsymbol{X} = \mathbf{x} | \boldsymbol{I}) = \frac{1}{Z(\boldsymbol{I})} exp\left( -\mathbb{E}(\mathbf{x}|\boldsymbol{I}) \right) $$

其中的 $\mathbb{E}(\mathbf{x}|\boldsymbol{I})$ 是能量函数，为了简便，以下省略全局观测 $\boldsymbol{I}$：

$$ E(\mathbf{x})=\sum_i{\Psi_u(x_i)}+\sum_{i,j}\Psi_p(x_i, x_j) $$

其中的一元势函数 $\sum_i{\Psi_u(x_i)}$ 即来自于前端FCN的输出。而二元势函数如下：

$$\Psi_p(x_i, x_j)=u(x_i, x_j)\sum_{m=1}^M{\omega^{(m)}k_G^{(m)}(\boldsymbol{f_i, f_j)}}$$

二元势函数就是描述像素点与像素点之间的关系，鼓励相似像素分配相同的标签，而相差较大的像素分配不同标签，而这个“距离”的定义与颜色值和实际相对距离有关。所以这样CRF能够使图片尽量在边界处分割。

而全连接条件随机场的不同就在于，二元势函数描述的是每一个像素与其他所有像素的关系，所以叫“全连接”。

Reference

  1. Harvard Referencing: Kamnitsas, K., Ledig, C., Newcombe, V.F., Simpson, J.P., Kane, A.D., Menon, D.K., Rueckert, D. and Glocker, B., 2017. Efficient multi-scale 3D CNN with fully connected CRF for accurate brain lesion segmentation. Medical image analysis, 36, pp.61-78.

  2. https://yq.aliyun.com/articles/232455

  3. https://zhuanlan.zhihu.com/p/22308032

 #

Like this article? Support the author with

Comments

Your browser is out-of-date!

Update your browser to view this website correctly.&npsb;Update my browser now

×

×