统计学习 - Statistical Learning
统计学习方法笔记总结。haven’t finished yet
1. k近邻法(k-Nearest Neighbors)
- 分类:在数据中找到与某个点(目标)最近的k个点,把该点(目标)的类分为k个点中多数的类。
回归:在数据中找到与某个点(目标)最近的k个点,k个点的均值为目标点的预测值。
优点:
- $k$ 近邻法是个非参数学习算法,它没有任何参数( $k$ 是超参数,而不是需要学习的参数)。
- 近邻模型具有非常高的容量,这使得它在训练样本数量较大时能获得较高的精度。
缺点:
- 计算成本很高。因为需要构建一个 $N \times N$ 的距离矩阵,其计算量为 $O(N^2)$,其中 $N$ 为训练样本的数量。
- 当数据集是几十亿个样本时,计算量是不可接受的。
- 在训练集较小时,泛化能力很差,非常容易陷入过拟合。
- 无法判断特征的重要性。
1.1 k近邻模型
- 模型由三个基本要素——距离度量、k值的选择和分类决策规则决定。
距离度量
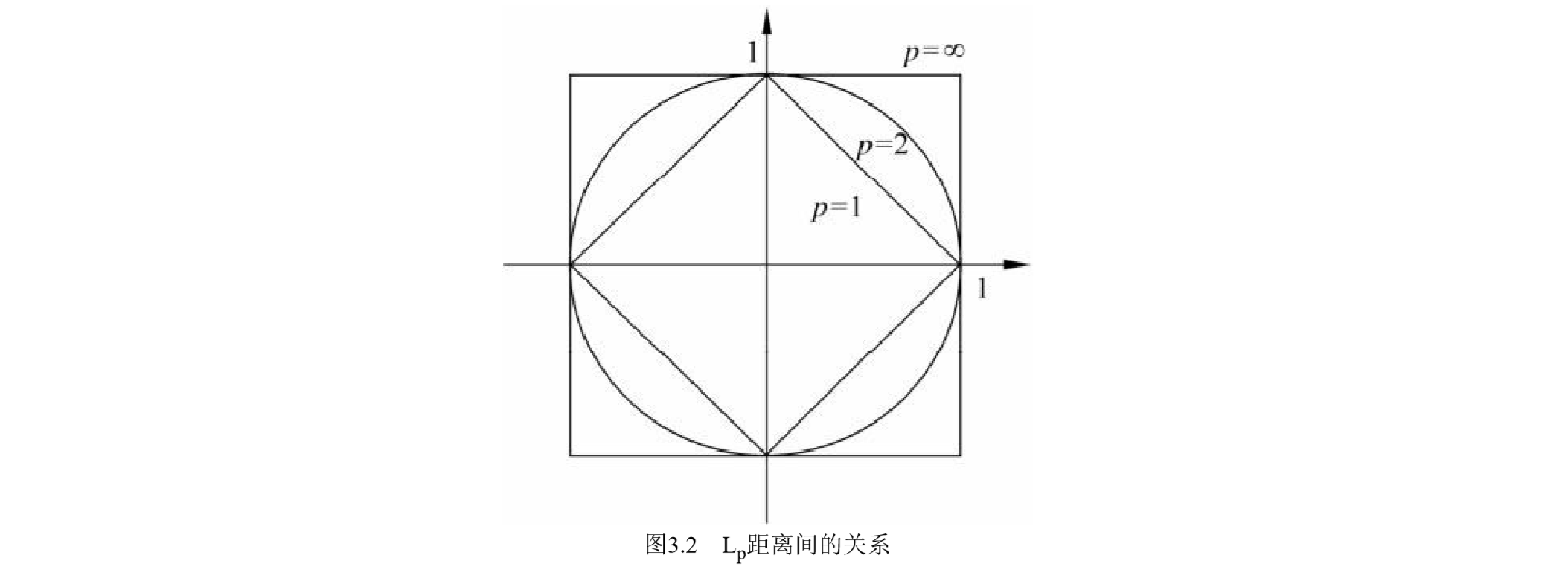
特征空间中两个实例点的距离是两个实例点相似程度的反映。k近邻模型的特征空间 一般是$n$维实数向量空间$\mathbb{R}^d$。使用的距离是欧氏距离,但也可以是其他距离,如更一般的$L_p$距离($L_p$ distance)或Minkowski距离(Minkowski distance)。
$$ L_p(\overrightarrow{\boldsymbol{x}_i},\ \overrightarrow{\boldsymbol{x}_j}) = \left( \sum_{l=1}^{n} |x_{i,l} - x_{j,l}|^p \right)^{1/p}\ , \quad \quad p \geqslant 1\\ \overrightarrow{\boldsymbol{x}_i}, \overrightarrow{\boldsymbol{x}_j} \in \mathcal{X}, \quad \overrightarrow{\boldsymbol{x}_i} = (x_i^{(1)}, x_i^{(2)}, \dots, x_i^{(d)})^T ,\quad {\boldsymbol{x}_j} = (x_j^{(1)}, x_j^{(2)}, \dots, x_j^{(d)})^T $$- 当 $p=2$ 时,称为欧氏距离(Euclidean distance):$L_2(\overrightarrow{\boldsymbol{x}_i},\ \overrightarrow{\boldsymbol{x}_j}) = \left( \sum_{l=1}^{n} |x_{i,l} - x_{j,l}|^2 \right)^{1/2}$
- 当 $p=1$ 时,称为曼哈顿距离(Manhattan distance):$L_1(\overrightarrow{\boldsymbol{x}_i},\ \overrightarrow{\boldsymbol{x}_j}) = \sum_{l=1}^{n} |x_{i,l} - x_{j,l}|$
- 当 $p=\infty$ 时,它是各个坐标距离的最大:$L_{\infty}(\overrightarrow{\boldsymbol{x}_i},\ \overrightarrow{\boldsymbol{x}_j}) = \underset{i}{\text{max}}|x_{i,l} - x_{j,l}|$
不同的距离度量所确定的最近邻点是不同的。
k值的选择
- k值的选择会对k近邻法的结果产生重大影响。
- 较小的k值:k值的减小就意味着整体模型变得复杂,容易发生过拟合。
相当于用较小的邻域中的训练实例进行预测,“学习”的近似 误差(approximation error)会减小,只有与输入实例较近的(相似的)训练实例才会对 预测结果起作用。但是“学习”的估计误差(estimation error)会增大,预测结果会对近邻的实例点非常敏感。如果邻近的实例点恰巧是噪声,预测就会出错。- 优点:减少”学习”的偏差。
- 缺点:增大”学习”的方差(即波动较大)。
- 较大的k值:k值的增大就意味着整体的模型变得简单。
相当于用较大邻域中的训练实例进行预测。其优点是可以减 少学习的估计误差。但缺点是学习的近似误差会增大。这时与输入实例较远的(不相似 的)训练实例也会对预测起作用,使预测发生错误。- 优点:减少”学习”的方差(即波动较小)。
- 缺点:增大”学习”的偏差。
- 应用中,k值一般取一个比较小的数值。通常采用交叉验证法来选取最优的k值。
- 较小的k值:k值的减小就意味着整体模型变得复杂,容易发生过拟合。
- k值的选择会对k近邻法的结果产生重大影响。
分类决策规则
- 分类决策规则往往是多数表决,即由输入实例的k个邻近的训练实例中的多数类决定输入实例的类。也可以基于距离的远近进行加权投票。
- 多数表决规则(majority voting rule)有如下解释:如果分类的损失函数为0-1损失函数,分类函数为 $$ \mathcal{f} : \mathbb{R}^d \rightarrow \{c_1, c_2, \dots, c_K \} $$ 对给定的实例$\overrightarrow{x} \in \mathcal{X}$,其最近邻的k个训练实例点构成集合$\mathcal{N}_k (\overrightarrow{x})$。如果涵盖$\mathcal{N}_k (\overrightarrow{x})$的区域的类别是cj,那么误分类率是 $$ L = \frac{1}{k} \sum_{\overrightarrow{x}_i \in \mathcal{N}_k (\overrightarrow{x})} I(\tilde{y}_i \neq c_m) = 1 - \frac{1}{k} \sum_{\overrightarrow{x}_i \in \mathcal{N}_k (\overrightarrow{x})} I(\tilde{y}_i = c_m) $$ $L$ 就是训练数据的经验风险。要使经验风险最小,则使得 $\sum_{\overrightarrow{x}_i \in \mathcal{N}_k (\overrightarrow{x})} I(\tilde{y}_i = c_m)$ 最大。即多数表决:$c_m = \underset{c_m}{\text{argmax}} \sum_{\overrightarrow{x}_i \in \mathcal{N}_k (\overrightarrow{x})} I(\tilde{y}_i = c_m)$。所以多数表决规则等价于经验风险最小化。
1.2 k近邻算法
- k近邻的分类算法:
- 输入:训练数据集 $$ D = \left\{ (\overrightarrow{\boldsymbol{x}}_1, y_1), (\overrightarrow{\boldsymbol{x}}_2, y_2), \dots, (\overrightarrow{\boldsymbol{x}}_n, y_n) \right\} $$ 其中,$\overrightarrow{\boldsymbol{x}}_i \in \mathcal{X} \subseteq \mathbb{R}^d$ 为实例的特征向量,$y_i \in \overrightarrow{\boldsymbol{y}} = \left\{ c_1, c_2, \dots, c_k \right\} $为实例的类别,$i = 1, 2, \dots, n$ 。
- 输出: 实例 $\overrightarrow{\boldsymbol{x}}$ 所属的类 y 。
- 步骤:
- 根据给定的距离度量,在训练集 $D$ 中找出与 $\overrightarrow{\boldsymbol{x}}$ 最邻近的k个点,涵盖这k个点的 $\overrightarrow{\boldsymbol{x}}$ 的邻域记作 $\mathcal{N}_k(\overrightarrow{\boldsymbol{x}})$ ;
- 在 $\mathcal{N}_k(\overrightarrow{\boldsymbol{x}})$ 中根据分类决策规则(如多数表决)决定 $\overrightarrow{\boldsymbol{x}}$ 的类别 $y$ :
$$
y = \underset{c_j}{\text{argmax}} \sum_{\overrightarrow{x}_i \in \mathcal{N}_k (\overrightarrow{x})} I(\tilde{y}_i = c_j), \quad i = 1, 2, \dots, n; \quad j = 1, 2, \dots, k
$$
- $I$ 为指示函数,即当$y_i=c_j$ 时 $I$ 为1,否则 $I$ 为0。
2. 朴素贝叶斯
朴素贝叶斯和贝叶斯分类(回归)器都是基于贝叶斯理论进行预测或者分类的模型。过程是利用训练数据学习 $P(X|Y)$ 和 $P(Y)$ 的估计,得到联合概率分布 $P(X,Y)=P(Y)P(X|Y)$ ,然后利用贝叶斯定理进行预测,将输入 $\overrightarrow{\boldsymbol{x}}$ 分到后验概率最大的类。
$$
P(Y|X) = \frac{P(X, Y)}{P(X)} = \frac{P(Y)P(X|Y)}{\sum_{Y}P(Y)P(X|Y)} \propto P(Y)P(X|Y) \\
\hat{y} = \underset{c_k}{\text{argmax }}P(Y=c_k) \prod_{j=1}^{d} P(X^{(j)} = x^{(j)} | Y = c_k)
$$
条件独立假设:
$$ \begin{aligned} P(X = \overrightarrow{\boldsymbol{x}}) & = \prod_{j=1}^{d} P(X^{(j)} = x^{(j)} | Y = c_k) \end{aligned} $$- 优点:
- 性能相当好,它速度快,可以避免维度灾难。
- 支持大规模数据的并行学习,且天然的支持增量学习。
- 缺点:
- 无法给出分类概率,因此难以应用于需要分类概率的场景。
2.1 贝叶斯定理
- 全概率公式 (Law of Total Probability Theorem):
- 贝叶斯定理 (Bayes’ theorem) 在数学上表示为以下等式:
2.2 朴素贝叶斯
朴素贝叶斯(naïve Bayes)法是基于贝叶斯定理与特征条件独立假设的分类方法。
2.2.1 基本方法及解释
2.2.1.1 基本方法
设输入空间 $X \subseteq R_n$ 为 $d$ 维向量的集合,输出空间为类标记集合 $y ={c_1, c_2, \dots, c_K}$。输入为特征向量$\overrightarrow{\boldsymbol{x}} \in X$ ,输出为类标记(class label)$y \in Y $ 。
$$ D = \left\{ (\overrightarrow{\boldsymbol{x}}_1, y_1), (\overrightarrow{\boldsymbol{x}}_2, y_2), \dots, (\overrightarrow{\boldsymbol{x}}_n, y_n) \right\} $$
$P(X,Y)$ 是 $X$ 和 $Y$ 的联合概率分布,训练数据集 $D$ 由 $P(X,Y)$ 独立同分布产生。步骤:
- 学习以下先验概率分布及条件概率分布。 $$ \begin{aligned} \text{(先验概率)} & \quad \quad P(Y=c_k), \quad \ k=1,2,\dots, k\\ \text{(条件概率)} & \quad \quad P(X = \overrightarrow{\boldsymbol{x}} | P(X^{(1)} = x^{(1)}, X^{(2)} = x^{(2)}, \dots, X^{(d)} = x^{(d)} | y = c_k) \end{aligned} $$
- 条件独立性的假设:
$$
\begin{aligned}
P(X = \overrightarrow{\boldsymbol{x}} | Y = c_k) & = P(X^{(1)} = x^{(1)}, X^{(2)} = x^{(2)}, \dots, X^{(d)} = x^{(d)} | y = c_k) \\
& = \prod_{j=1}^{d} P(X_j = x^{(j)} | Y = c_k)
\end{aligned}
$$
- 条件独立假设等于 是说用于分类的特征在类确定的条件下都是条件独立的。这一假设使朴素贝叶斯法变得简单,但有时会牺牲一定的分类准确率。
- 朴素贝叶斯法分类时,对给定的输入 $\overrightarrow{\boldsymbol{x}}$ ,通过学习到的模型计算后验概率分布 $P(Y= c_k|X=\overrightarrow{\boldsymbol{x}})$。 $$ \begin{aligned} P(Y = c_k | X = \overrightarrow{\boldsymbol{x}}) & = \frac{P(X = \overrightarrow{\boldsymbol{x}} | Y = c_k)}{\sum_{k} P(X = \overrightarrow{\boldsymbol{x}} | Y = c_k)}\\ \text{(独立性假设)} & = \frac{P(Y = c_k)\prod_{j=1}^{d} P(X_j = x^{(j)} | Y = c_k)}{\sum_{k} P(Y = c_k)\prod_{j=1}^{d} P(X_j = x^{(j)} | Y = c_k)}, \quad k = 1,2,\dots,K \end{aligned} $$
- 将后验概率最大的类作为x的类输出:
$$
\begin{aligned}
\hat{y} = f(\overrightarrow{\boldsymbol{x}}) = \underset{c_k}{\text{argmax }} P(Y = c_k) \prod_{j=1}^{d} P(X_j = x^{(j)} | Y = c_k)
\end{aligned}
$$
- Note:因为后验概率的分母都相同,因此在这可以忽略。
2.2.1.2 后验概率最大的含义等价于期望风险最小化 (Optional)
- 假设选择 0-1损失函数: $$ \begin{aligned} L(Y, f(X)) = \begin{cases} 0, \quad \ Y = f(X)\\ 1, \quad \ Y \neq f(x) \end{cases} \end{aligned} $$
- 期望风险函数 $$ \begin{aligned} R_{exp}(f) = \mathbb{E} \left[ L(Y, f(X)) \right] = \sum_{\overrightarrow{\boldsymbol{x}}}\sum{y \in Y} L(y, f(\overrightarrow{\boldsymbol{x}})) P(\overrightarrow{\boldsymbol{x}}, y) = \mathbb{E}_X \left[ \sum_{y \in Y} L(y, f(\overrightarrow{\boldsymbol{x}})) P(y | \overrightarrow{\boldsymbol{x}}) \right] \end{aligned} $$
- 为了使期望风险最小化,只需对 $\overrightarrow{\boldsymbol{x}}$ 逐个极小化 $$ \begin{aligned} f(\overrightarrow{\boldsymbol{x}}) & = \underset{y \in Y}{\text{argmin}} \sum_{k} L(c_k, y) P(y = c_k | X = \overrightarrow{\boldsymbol{x}})\\ & = \underset{y \in Y}{\text{argmin}} \sum_{k} P(y \neq c_k | X = \overrightarrow{\boldsymbol{x}})\\ & = \underset{y \in Y}{\text{argmin}} \sum_{k} (1 - P(y = c_k | X = \overrightarrow{\boldsymbol{x}}))\\ & = \underset{y \in Y}{\text{argmax}} \sum_{k} P(y = c_k | X = \overrightarrow{\boldsymbol{x}}) \end{aligned} $$
2.2.1.3 参数估计 - 极大似然估计
朴素贝叶斯中可以利用极大似然估计先验概率和条件概率。
$$
\begin{aligned}
P(Y = c_k) \frac{1}{n} \sum_{i=1}^{n} I(y_i = c_k)\\
P(X^{(j)} = a_{jl} \ |\ Y = c_k) = \frac{\sum_{i=1}^{n} I\left( x_i^{(j)} = a_{jl} \ |\ y_i = c_k \right)}{\sum_{i=1}^{n} I(y_i=c_k)}\\
j = 1, 2, \dots, d; \quad l = 1, 2, \dots, S_j; \quad k = 1, 2, \dots, K
\end{aligned}
$$
其中,$x_i^{(j)}$ 是第 $i$ 个样本的第 $j$ 个特征;$a_{jl}$ 是第 $j$ 个特征可能取的第 $l$ 个值;$I$ 为指示函数。
2.2.1.4 贝叶斯估计
用极大似然估计可能会出现所要估计的概率值为0的情况。解决这一问题的方法是采用贝叶斯估计。具体地,条件概率的贝叶斯估计(or also known as add-alpha smoothing)是
$$ \begin{aligned} P_{\alpha}(X^{(j)} = a_{jl} | Y = c_k) = \frac{\sum_{i=1}^{n} I\left( x_i^{(j)} = a_{jl} | y_i = c_k \right) + \alpha}{\sum_{i=1}^{n} I(y_i=c_k) + S_j \alpha}\\ \end{aligned} $$其中,$\alpha \geqslant 0$
- 当 $\alpha = 0$ 为极大似然估计,当 $\alpha = 1$为拉普拉斯平滑(Laplace smoothing, also known as add-one smoothing)。
2.2.2 算法
朴素贝叶斯算法(naïve Bayes algorithm)
利用极大使然估计先验概率 $P(Y = c_k)$ 和条件概率 $P(X^{(j)} = a_{jl} \ |\ Y = c_k)$,如Sec 2.2.1.2
对于给定的实例 $\overrightarrow{\boldsymbol{x}}=(x^{(1)},x^{(2)},…,x^{(d)})^T$ ,计算
$$ \begin{aligned} P(Y = c_k)\prod_{j=1}^{d} P(X_j = x^{(j)} \ |\ Y = c_k), \quad \ k = 1, 2, \dots, K \end{aligned} $$- 确定实例 $\overrightarrow{\boldsymbol{x}}$ 的类 $$ \hat{y} = \underset{c_k}{\text{argmax}} \ P(Y = c_k)\prod_{j=1}^{d} P(X_j = x^{(j)} \ |\ Y = c_k) $$
例子:

3. 支持向量机
支持向量机(support vector machines,SVM)是一种二类分类模型。它的基本模型是定义在特征空间上的间隔最大的线性分类器。支持向量机的学习算法是求解凸二次规划的最优化算法。
间隔最大使它有别于感知机;
感知机利用误分类最小的策略,求得分离超平面,不过这时的解有无穷多个。线性可分支持向量机利用间隔最大化求最优分离超平面,这时,解是唯一的。
支持向量机还支持核技巧,从而使它成为实质上的非线性分类器。
支持向量机学习方法包含构建由简至繁的模型:
- 当训练数据线性可分时,通过硬间隔最大化(hard margin maximization),学习一个线性的分类器,即线性可分支持向量机,又称为硬间隔支持向量机;
- 当训练数据近似线性可分时,通过软间隔最大化(soft margin maximization),也学习一个线性的分类器,即线性支持向量机,又称为软间隔支持向量机;
- 非线性支持向量机;当训练数据线性不可分时,通过使用核技巧(kernel trick)及软间隔最大化,学习非线性支持向量机
- 特征向量之间的内积就是核函数,使用核函数可以学习非线性支持向量机。
- 非线性支持向量机等价于隐式的在高维的特征空间中学习线性支持向量机,这种方法称作核技巧。
3.1 线性可分支持向量机
- 假设给定一个特征空间上的训练数据集
$$
D = \left\{ (\overrightarrow{\boldsymbol{x}}_1, y_1), (\overrightarrow{\boldsymbol{x}}_2, y_2), \dots, (\overrightarrow{\boldsymbol{x}}_n, y_n) \right\}
$$
其中,$\overrightarrow{\boldsymbol{x}}_i \in \mathcal{X} \subseteq \mathbb{R}^d$, $y_i \in {-1, +1}, \; i=1,2,\dots,n$ .
$\overrightarrow{\boldsymbol{x}}_i$ 为第 $i$ 个(d维)特征向量,也称为实例,$(x_i,\ y_i)$ 称为样本点。 - 假设数据集线性可分。则学习的目标是在特征空间中找到一个分离超平面,能将实例分到不同的类。分离超平面对应于方程$\boldsymbol{W}_{k \times d} \cdot \overrightarrow{\boldsymbol{x}} + \overrightarrow{\boldsymbol{b}}$,它由法向量 $\boldsymbol{W}$ 和截距 $\overrightarrow{\boldsymbol{b}}$ 决定,可用 $(\boldsymbol{W},\overrightarrow{\boldsymbol{b}})$ 来表示。例如:
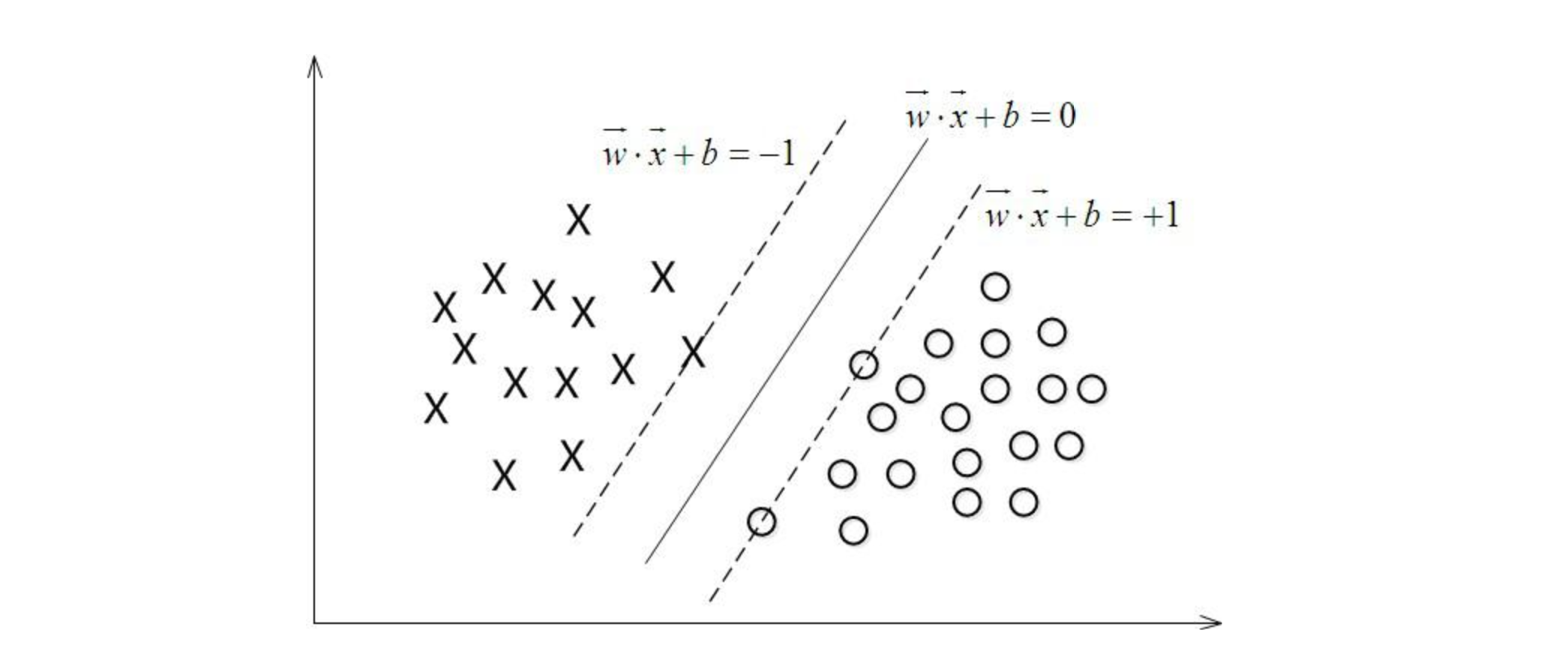
- 给定线性可分训练数据集,通过间隔最大化或等 价地求解相应的凸二次规划问题学习得到的分离超平面为 $\boldsymbol{W}^{*} \cdot \overrightarrow{\boldsymbol{x}} + \overrightarrow{\boldsymbol{b}^{*}} = 0$ 以及相应的分类决策函数 $f(\overrightarrow{\boldsymbol{x}}) = sign( \boldsymbol{W}^{*} \cdot \overrightarrow{\boldsymbol{x}} + \overrightarrow{\boldsymbol{b}^{*}} )$
3.1.1 函数间隔
- 对于给定的训练数据集 $D$ 和超平面 $(\boldsymbol{W},\overrightarrow{\boldsymbol{b}})$ ,定义超平面 $(\boldsymbol{W},\overrightarrow{\boldsymbol{b}})$ 关于样本点 $(\overrightarrow{\boldsymbol{x}}_i,y_i)$ 的函数间隔为 $$\hat{\gamma}_i = y_i (\boldsymbol{W} \cdot \overrightarrow{\boldsymbol{x}}_i + \overrightarrow{\boldsymbol{b}} )$$ 定义超平面 $(\boldsymbol{W},\overrightarrow{\boldsymbol{b}})$ 关于训练数据集 $D$ 的函数间隔为超平面关于 $D$ 中所有样本点 $(x_i,y_i)$ 函数间隔之最小值,即 $$\hat{\gamma} = \underset{i = 1, \dots , n}{\text{min}} \hat{\gamma}_i$$
可以将一个点距离分离超平面的远近来表示分类预测的可靠程度:
- 一个点距离分离超平面越远,则该点的分类越可靠。
- 一个点距离分离超平面越近,则该点的分类则不那么确信。
在超平面 $\boldsymbol{W} \cdot \overrightarrow{\boldsymbol{x}} + \overrightarrow{\boldsymbol{b}} = 0$ 确定的情况下:
- $| \boldsymbol{W} \cdot \overrightarrow{\boldsymbol{x}}_i + \overrightarrow{\boldsymbol{b}}| $ 能够相对地表示点 $\overrightarrow{\boldsymbol{x}}_i$ 距离超平面的远近。
3.1.2 几何间隔
因为只要成比例地改变 $\boldsymbol{W}$ 和 $b$ ,例如将它们改为 $2w$ 和 $2b$ ,超平面并没有改变,但函数间隔却成为原来的2倍。这一事实启示我们,可以对分离超平面的法向量 $\boldsymbol{W}$ 加某些约束,如规范化,$||\boldsymbol{W}||= 1$ ,使得间隔是确定的。这时函数间隔成为几何间隔(geometric margin)。
对于给定的训练数据集 $D$ 和超平面 $(\boldsymbol{W},\overrightarrow{\boldsymbol{b}})$ ,定义超平面 $(\boldsymbol{W},\overrightarrow{\boldsymbol{b}})$ 关于样本点 $(\overrightarrow{\boldsymbol{x}}_i,y_i$ 的几何间隔为 $$\hat{\gamma}_i = y_i (\frac{\boldsymbol{W}}{||\boldsymbol{W}||} \cdot \overrightarrow{\boldsymbol{x}}_i + \frac{\overrightarrow{\boldsymbol{b}}}{||\boldsymbol{W}||} )$$ 定义超平面 $(\boldsymbol{W},\overrightarrow{\boldsymbol{b}})$ 关于训练数据集 $D$ 的几何间隔为超平面关于 $D$ 中所有样本点 $(x_i,y_i)$ 几何间隔之最小值,即 $$\hat{\gamma} = \underset{i = 1, \dots , n}{\text{min}} \hat{\gamma}_i$$
由定义可知函数间隔和几何间隔有下列的关系:
$$\gamma_i = \frac{\hat{\gamma}_i}{||W||}; \quad \gamma = \frac{\hat{\gamma}}{||W||}$$- 当 $||\boldsymbol{W}|| = 1$ 时,函数间隔和几何间隔相等。
- 如果超平面参数 $\boldsymbol{W}$ 和 $\overrightarrow{\boldsymbol{b}}$ 成比例地改变(超平面没有改变),函数间隔也按此比例改变,而几何间隔不变。
3.1.3 硬间隔最大化
- 间隔最大化的直观解释是:对训练数据集找到几何间隔最大的超平面意味着以充分大的确信度对训练数据进行分类。
- 几何间隔最大化的物理意义:不仅将正负实例点分开,而且对于最难分辨的实例点(距离超平面最近的那些点),也有足够大的确信度来将它们分开。
- 求解一个几何间隔最大的分离超平面的问题可以表示为下面的约束最优化问题: $$ \begin{aligned} & \underset{\boldsymbol{W}, \overrightarrow{\boldsymbol{b}}}{\text{max}} & & \gamma \\ & \text{s.t.} & & y_i (\frac{\boldsymbol{W}}{||\boldsymbol{W}||} \cdot \overrightarrow{\boldsymbol{x}}_i + \frac {\overrightarrow{\boldsymbol{b}}}{||\boldsymbol{W}||} ) \geqslant \gamma ; \quad i=1,2,\dots,n \end{aligned} $$ 考虑几何间隔和函数间隔的关系式(7.8),可将这个问题改写为 $$ \begin{aligned} & \underset{\boldsymbol{W}, \overrightarrow{\boldsymbol{b}}}{\text{max}} & & \frac{\hat{\gamma}}{||\boldsymbol{W}||} \\ & \text{s.t.} & & y_i (\boldsymbol{W} \cdot \overrightarrow{\boldsymbol{x}}_i + \overrightarrow{\boldsymbol{b}} ) \geqslant \hat{\gamma} ; \quad i=1,2,\dots,n \end{aligned} $$
Reference
- 李航. 统计学习方法[M]. 清华大学出版社, 2012年3月.
- Ai算法工程师手册